- Assertions
- MergeSort
- Botton-up MergeSort
- Sorting Complexity
- Java: Comparator interface
- Stability
Assertions
// after sort
assert isSorted(a, lo, hi);
Can enable or disable at runtime
# enable assertions
$ java -ea MyProgram
# disable assertions (default)
$ java -da MyProgram
Best practices
- Use assertions to check internal invariants
- assume assertions will be disabled in production code
- do not use for external argument checking
MergeSort
Animation: Merge Sort
Implement
public class MergeSort{
/**
* Interface
**/
public static void mergeSort(Comparable[] a){
Comparable[] aux = new Comparable[a.length];
mergeSort(a, aux, 0, a.length -1);
}
/**
* Recursion method
*
* Parameters:
* a: data
* aux: buffer
* lo: sort start at
* hi: sort end with
**/
private static void mergeSort(Comparable[] a, Comparable[] aux, int lo, int hi){
if (lo >= hi) return;
int mid = (lo + hi) / 2;
p("mergeSort: [" + lo + ", " + mid + "]");
mergeSort(a, aux, lo, mid);
p("mergeSort: [" + (mid+1) + ", " + hi + "]");
mergeSort(a, aux, mid + 1, hi);
p("merge: [" + lo + ", " + mid + "] + [" + (mid+1) + ", " + hi + "] -> [" + lo + ", " + hi + "]");
merge(a, aux, lo, mid, hi);
}
/**
* Merge two sub-arrays into one: aux[lo, mid] + aux[mid + 1, hi] -> arr[lo, hi]
*
* Parameters:
* a: target data
* aux: source data, buffer
* lo: source 1 start at
* mid: source 1 end with, source 2 start at mid+1
* hi: source 2 end with
**/
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi){
for (int i = lo; i <= hi; i++){
aux[i] = a[i];
}
// count: point to target array
int count = lo;
// lm: point to arr[lo, mid]
int lm = lo;
// mh: point to arr[mid+1, hi]
int mh = mid + 1;
while(count <= hi){
if (lm > mid) a[count++] = aux[mh++];
else if (mh > hi) a[count++] = aux[lm++];
else if (less(aux[lm], aux[mh])) a[count++] = aux[lm++];
else a[count++] = aux[mh++];
// == else if (aux[lo] > aux[mid + 1])
}
}
public static boolean less(Comparable a, Comparable b){
return a.compareTo(b) < 0;
}
// unit test
public static void main(String[] args){
// int[] will cause error, since int is not Comparable. Auto-boxing do not cover this case
Integer[] a = {4,2,52,3,5,1,2,23,9,20,0};
mergeSort(a);
for (int i : a){
System.out.print(i + ", ");
}
System.out.println();
}
public static void p(String s){
System.out.println(s);
}
}
Cost
Time
Mergesort uses at most N lg N compares and 6 N lg N array accesses to sort any array of size N
Space
Mergesort uses extra space proportional to N.
A sorting algorithm is in-place if it uses ≤ c log N extra memory. Ex. Insertion sort, selection sort, shellsort.
Improvements
Use insertion sort for small subarrays.
- Mergesort has too much overhead for tiny subarrays.
- Cutoff to insertion sort for ≈ 7 items.
private static void cutOffSort(Comparable[] a, Comparable[] aux, int lo, int hi) {
int CUTOFF = 7; // 7 is fine
// length = hi - lo + 1
if (hi - lo + 1 <= CUTOFF) {
Insertion.sort(a, lo, hi);
return;
}
int mid = lo + (hi - lo) / 2;
sort (a, aux, lo, mid);
sort (a, aux, mid+1, hi);
merge(a, aux, lo, mid, hi);
}
will make it maybe 20% faster.
Stop if sorted: max item of first half is smaller than right half.

private static void mergeSort(Comparable[] a, Comparable[] aux, int lo, int hi){
if (lo >= hi) return;
int mid = (lo + hi) / 2;
mergeSort(a, aux, lo, mid);
mergeSort(a, aux, mid + 1, hi);
// max item of first half is smaller than right half, so it is already sorted
if (less(a[mid], a[mid + 1])) return;
merge(a, aux, lo, mid, hi);
}
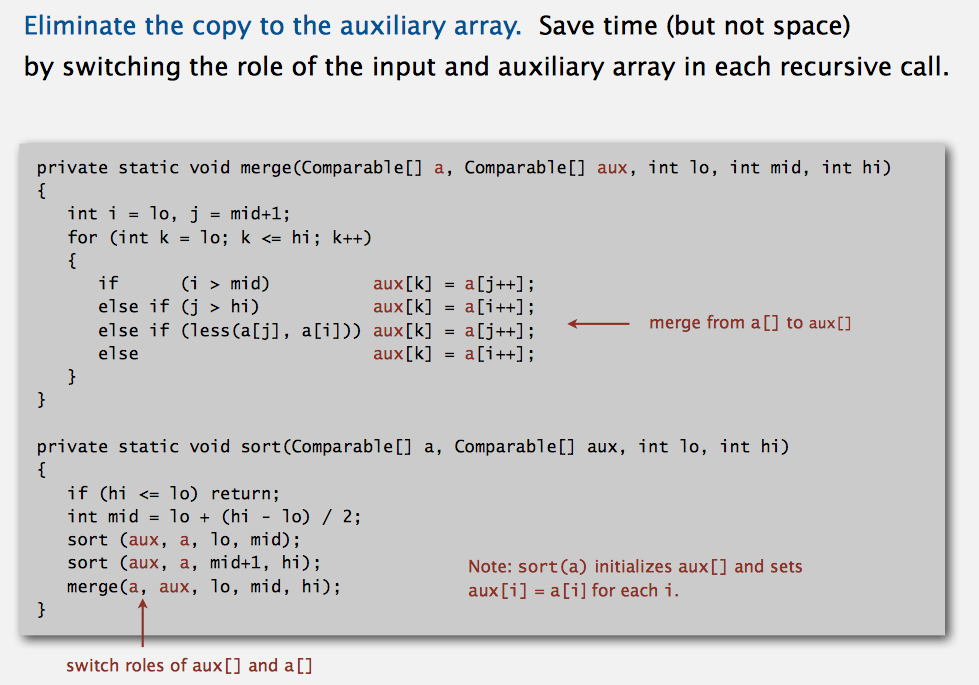
Eliminate the copy to the auxiliary array.
// TODO: 不懂?
Botton-up MergeSort
Remove recursive.
public static void mergeSortWithoutRecursive(Comparable[] a){
int N = a.length;
Comparable[] aux = new Comparable[N];
for (int sz = 1; sz < N; sz *= 2){
for (int lo = 0; lo < N - sz; lo += sz*2)
merge(a, aux, lo, lo+sz-1, Math.min(lo+2*sz-1, N-1));
}// end for size
}
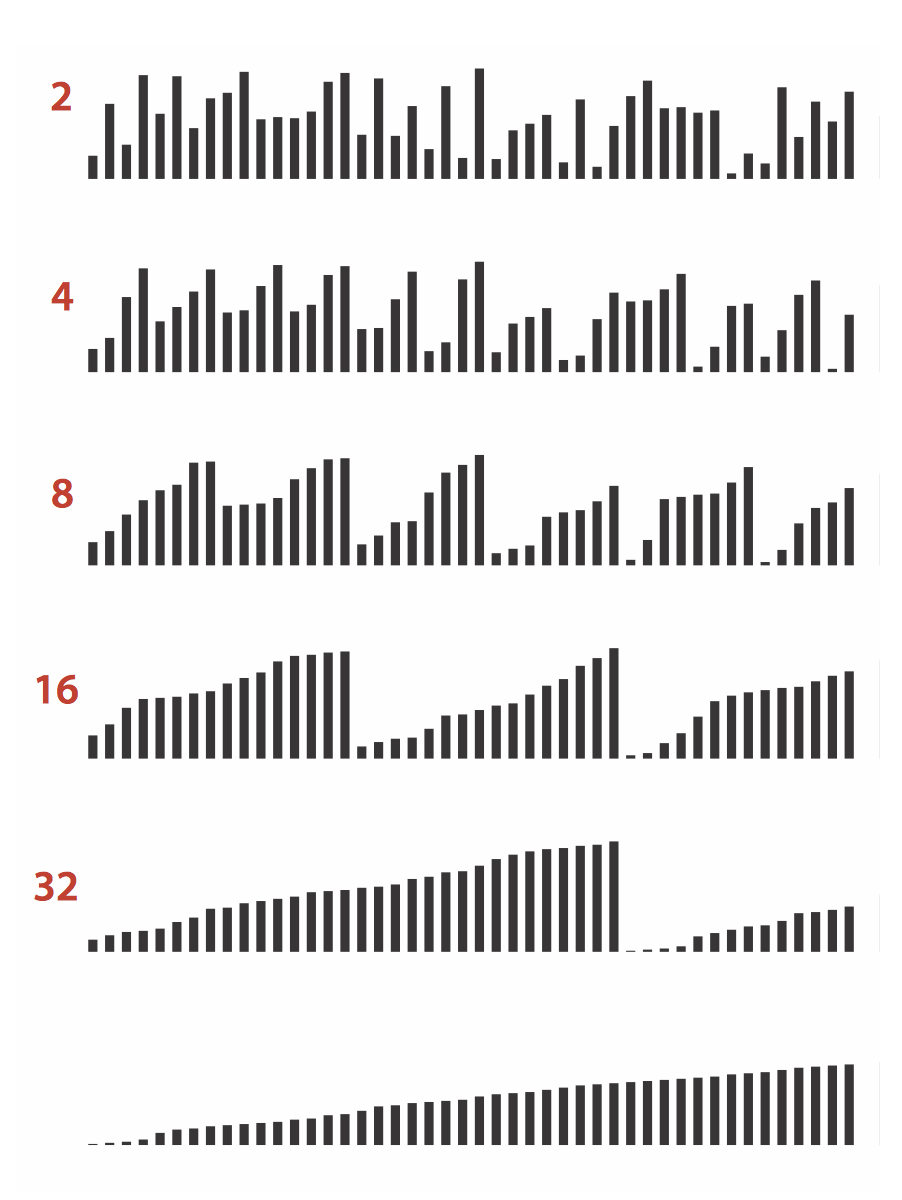
- It does not always divide by half. So a part might be small than other(s).
- 10% slower than recursive, top-down mergesort on typical systems
- get log(2)(n) passes(遍历)
Complexity
-
Model of computation: Allowable operations
-
Cost model: Operation count(s)
-
Upper bound: Cost guarantee provided by some algorithm for X (current algorithms can achieve)
-
Lower bound: Proven limit on cost guarantee of all algorithms for X (future possible algorithms can maximumly achieve)
-
Optimal algorithm: Algorithm with best possible cost guarantee for X (this algorithm is the best)
Sort Complexity
- Model of computation: decision tree (can access information only through compares; example below)
- Cost model: # compares.
- Upper bound: ~ N lg N from mergesort
- Lower bound: N lg N
- Optimal algorithm: mergesort
Decision tree
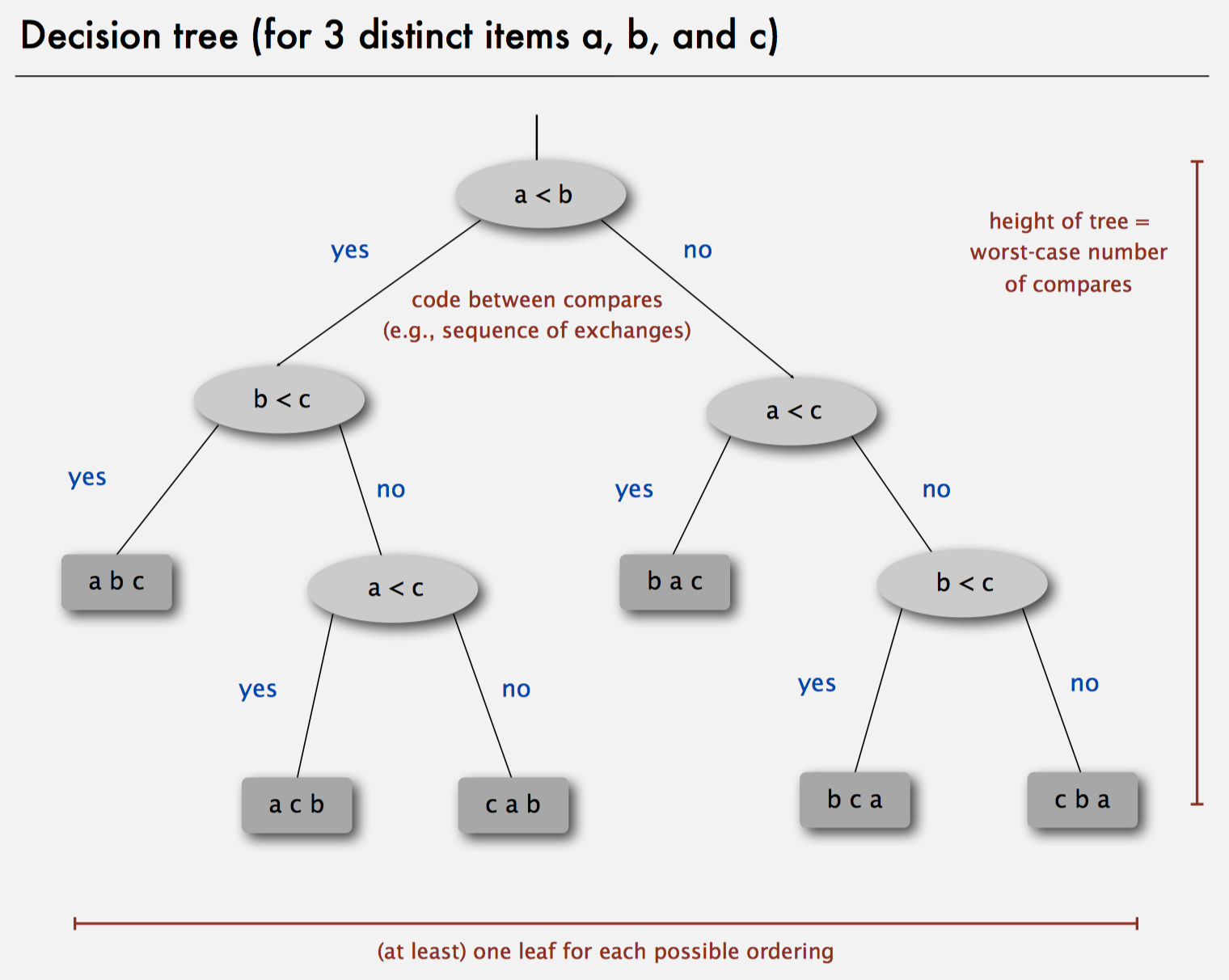
- Height: Worst case: 3 compares. Aka, the height of decision tree.
- Leaf: each possible ordering
Lower bound
We can proof that any compare-based sort algorithm must use at least N lg N compares in the worst-case.
Pf.
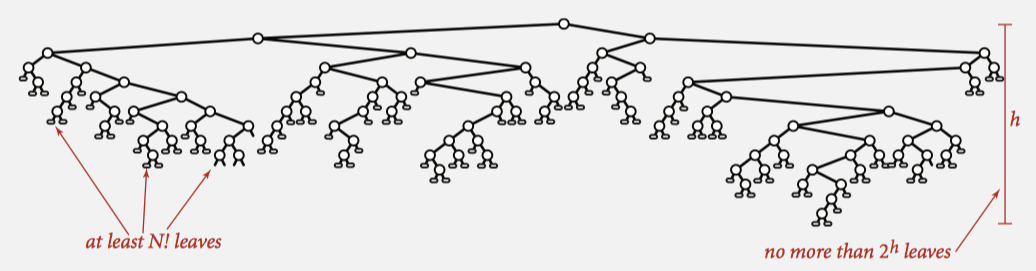
leaves = N! max hight = lg N! (log(2)(N!)) => lg(N!) = N lg N (Stirling’s formula)
Optimal algorithm
Since mergesort has a cost of N lg N in the worst-case. So it’s the best algorithm. But mergesort is not good at Space cost. It cost twice N.
In some particular cases, MergeSort may not be the best:
- Partially-ordered arrays. Depending on the initial order of the input, we may not need N lg N compares. Ex. insertion sort requires only N-1 compares if input array is sorted.
Java: Comparator interface
Usage:
public static void sort(Object[] a, Comparator comparator) {
int N = a.length;
for (int i = 0; i < N; i++)
for (int j = i; j > 0 && less(comparator, a[j], a[j-1]); j--)
exchange(a, j, j-1);
}
private static boolean less(Comparator c, Object v, Object w) { return c.compare(v, w) < 0; }
private static void exchange(Object[] a, int i, int j) { Object swap = a[i]; a[i] = a[j]; a[j] = swap;
Implement:
public class Student {
public static final Comparator<Student> BY_NAME = new ByName();
public static final Comparator<Student> BY_SECTION = new BySection();
private final String name;
private final int section;
private static class ByName implements Comparator<Student> {
public int compare(Student v, Student w) {
return v.name.compareTo(w.name); }
}
…
private static class BySection implements Comparator<Student> {
public int compare(Student v, Student w) {
return v.section - w.section; }
}
Stability
Ex. for unstable
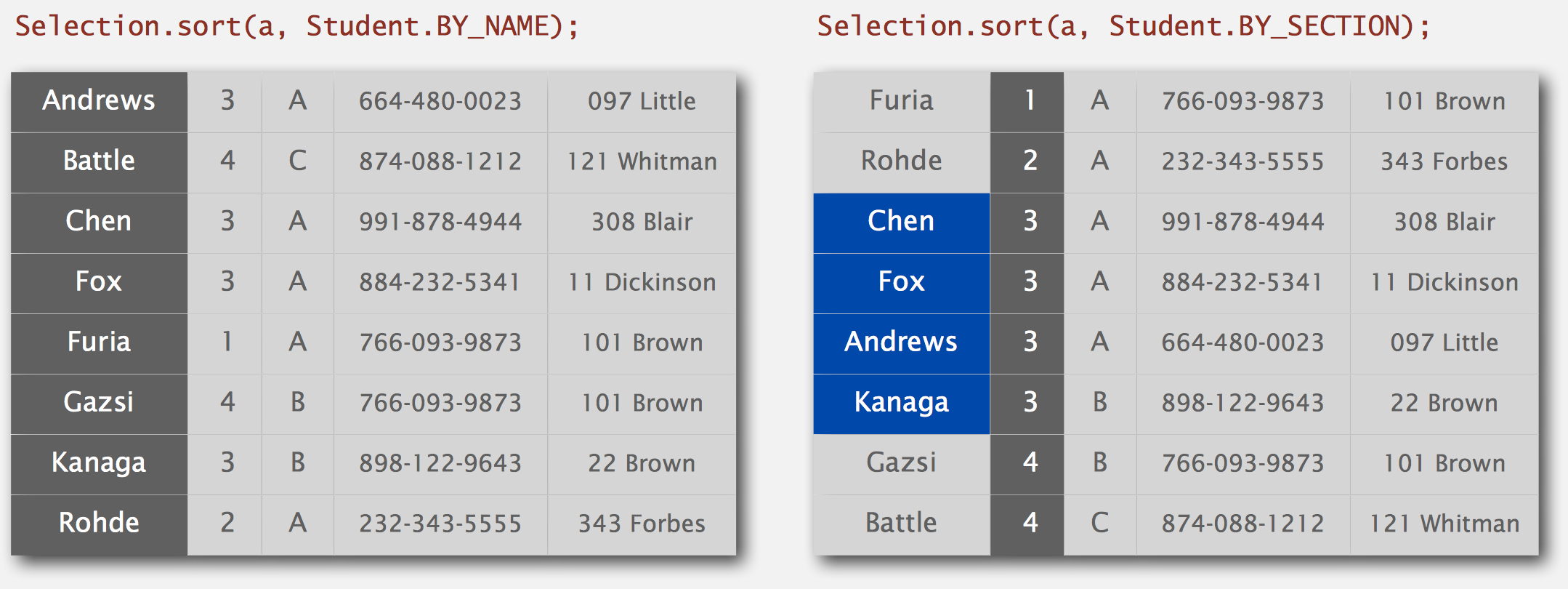
After sort, students in section 3 no longer stay sorted by name.
What is Stable?
- A stable sort preserves the relative order of items with equal keys
- Never move equal items pass one another
Stable sort:
- insertion sort
- mergesort
Unstable sort:
- selection sort
- shellsort
Why is Selection Sort not stable?
A small example:
Let b = B in
< B > , < b > , < a > , < c > (with a < b < c)
After one cycle the sequence is sorted but the order of B and b has changed:
< a > , < b > , < B > , < c >