• Comparable
• Selection Sort
• Insertion Sort
• Shell Sort
• Shuffle
• Convex hull

Comparable

Implement the Comparable interface to make the sort() universal.

public class File implements Comparable<File>{
…
    public int compareTo(File b){
        …
        return -1; // this less than b
        …
        return +1; // this greater than b
        …
        return 0; // equal
    }
…
}

public static void sort(Comparable[] a){
    int N = a.length;
    for (int i = 0; i < N; i++){
        for (int j = i; j > 0; j--){
            if (a[j].compareTo(a[j-1]) < 0)
                exchange(a,j,j-1);
            else break; // compare to next
        }// end for j
    }// end for i
}// end sort()

Selection sort

• In iteration i, find index min of smallest remaining entry.
• Swap a[i] and a[min]

public static void sort(Comparable[] a){
    int N = a.lengh;
    for (int i = 0; i < N; i++){
        int min = i;
        for (int j = i+1; j < N; j++)
            if (less(a[j], a[min]) min = j;
        exchange(a, i, min);
    }// end for i
}// end sort()

Facts

• Running time is insensitive to input: always quadratic time
• Data movement is minimal: linear number of exchanges(one-step to its final position)

Insertion Sort

Animation: Insertion Sort

public static void sort(Comparable[] a){
    int n = a.length;
    // although start with 0 is waste of time, think about if n = 0, 1 will cause mistake, you need another `if` statement to proof it
    for (int i = 0; i < n; n++){
        for (int j = i; j > 0; j--){
            if (less(a[j], a[j-1]) exchange(a, j, j-1);
            // all before is already sorted, so do break
            else break;
        }// end for j
    }// end for i
}// end sort()

Facts

It’s obviously that this sort is highly depend on the data.

• Best case: already in order. N-1 compares, 0 exchange.
• Worst case: reversed order. N(1+N)/2 compares, N(1+N)/2 exchanges. ~1/2 N^2
• Partially-sorted: linear. ~N. This feature will be used in the ‘Shellsort’

Shellsort

Insertion sort is kind of waste: each time comparing with the the only 1-before item although the j might be very small — considering the reverse case.

So we can jump. Compare to k-before item; If bigger, exchange. The result will be h-sort. Like this:

every 4 interleaved item is sorted: L, M, P, T; E, H, S, S; … The result will be nearly ordered.

imply h-sort with different h:

A g-sorted array remains g-sorted after h-sorting it.

It’s quiet nature. I’m not going to proof it..

After 3-sort, we can imply 1-sort, aka, original insertion sort. After that, the array will become sorted.

This algorithm is more efficient. The problem is how to determine the h?

• 2^i: 1, 2, 4, 8, 16, 32, … (BAD: ignore the even position until final 1-sort, the even position may remain very unstable)
• 2^i - 1: 1, 3, 7, 15, 31, 63, … (MAYBE)
• 3x + 1(x is the previous one): 1, 4, 13, 40, 121, 364, … (OK)
• Sedgewick (merging of (9 ⨉ 4 i ) – (9 ⨉ 2 i ) + 1 and 4 i – (3 ⨉ 2 i ) + 1): 1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905, … (GOOD)

Animation: Shell Sort

Implement

public static void shellSort(Comparable a[]){
    int n = a.length;
    // in the cycle we do not have another check. we start with h
    if (n == 0) return;
    int h = 1;
    // minium sub-sort array length is 3
    while (h < n/3) h = h * 3 + 1; 
    
    // until 1-sort
    while (h > 0){
        for (int i = h; i < n; i++){
            for (int j = i; j >= h; j-=h){
                if (less(a[j], a[j-h])) exchange(a, j, j-h);
                else break;
            }// end for j
        }// end for i
    h /= 3; // h = h / 3; === h = (h - 1) / 3
    // 1, 4, 13, 40, 121, 364, ...
    }// end while h
}// end sort()

A more beautiful code:

for (int j = i; j >= h; j-=h){
    if (less(a[j], a[j-h])) exchange(a, j, j-h);
    else break;
}// end for j
// === equal to ===
for (int j = i; j >= h && less(a[j], a[j-h]); j -= h)
    exchange(a, j, j-h);

we do not need a else break; ‘cause the statement is in the rules line.

Cost

• worst-case with 3x + 1 : O(N^3/2)
• avg with 3x + 1: NlgN ( it’s a guess, accurate model has not yet been discovered)

Useful in practice:

• Fast unless array size is huge (used for small subarrays).
• Tiny, fixed footprint for code (used in some embedded systems).
• Hardware sort prototype.

Unsolved questions:

• Asymptotic growth rate?
• Best sequence of increments?
• Average-case performance?

Q: Does prime number is a good increments?

(Q: 素数是不是一个比较好的 increments?) A: No 实验见 Algs-part1-coursera/week-2-stack-queue/prime-shellsort at master · d4rkb1ue/Algs-part1-coursera · GitHub

$ java-algs4 PrimeShellSort < int30000.txt 
size: 30000
3x + 1 in 0.014s
prime in 0.109s
$ java-algs4 PrimeShellSort < int30000.txt 
size: 30000
3x + 1 in 0.015s
prime in 0.101s
$ java-algs4 PrimeShellSort < int30000.txt 
size: 30000
3x + 1 in 0.014s
prime in 0.108s
$ java-algs4 PrimeShellSort < int30000.txt 
size: 30000
3x + 1 in 0.015s
prime in 0.104s

Shuffle

A simply solution is set each item with a random number, and then, base on the giving number to sort these items. However, it’s quiet waste. Sort is very expansive.

public void shuffle(Object[] a){
    int n = a.length;
    for (int i = 0; i < n; i++){
        // exchange with [0,i]
        exchange(a, i, StdRandom.uniform(i + 1));
    }
}

You should exchange with [0, i] instead of [0, n] because [i+1, n-1] is unseen, doing a whole array doesn’t give you a uniformly random result.

Why exchange(a, i, random[0,n)) is not correct?

algorithms - What’s a uniform shuffle? - Computer Science Stack Exchange http://stats.stackexchange.com/questions/3082/what-is-wrong-with-this-naive-shuffling-algorithm

Wrong practice

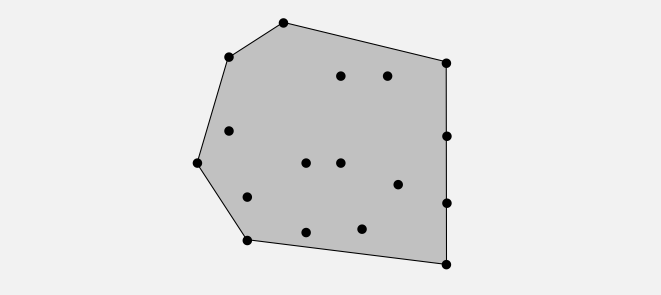
Convex hull

The convex hull of a set of N points is the smallest perimeter fence enclosing the points.