algs4.jar/Stopwatch

public static void main(String[] args){
   int[] a = In.readInts(args[0]);
   Stopwatch stopwatch = new Stopwatch();
   StdOut.println(ThreeSum.count(a));
   double time = stopwatch.elapsedTime(); // time since creation (in seconds)
}

复杂度计算

Log-log plot

For given data like in standard plot,

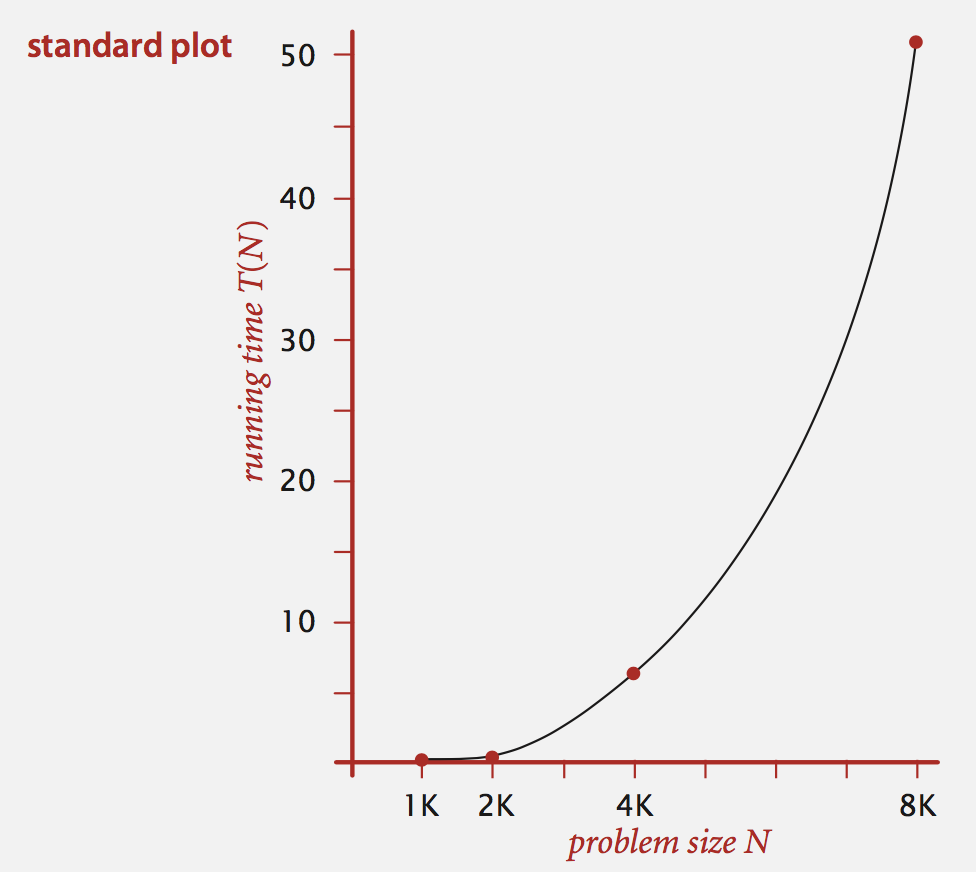
way to find out its T(N) is by: Log-log plot:

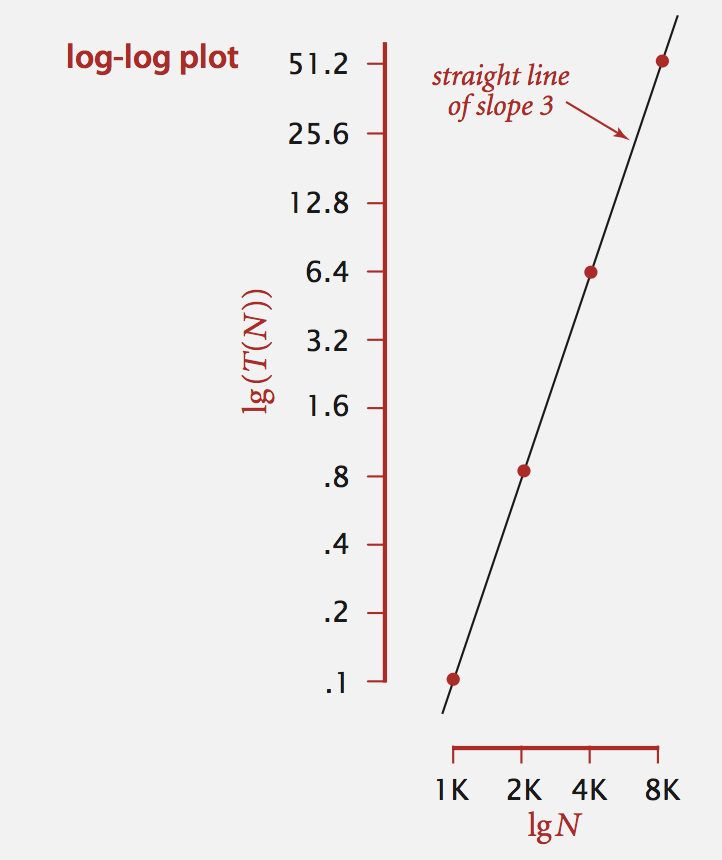
where we calculate by

lg(T (N)) = b lg N + c 
T (N) = a N^b, where a = 2^c

in this case,

b = 2.999
c = -33.2103

so,

T(N) = 1.006 × 10^–10 × N^2.999

Assume b = 3, run multi times to estimate a.

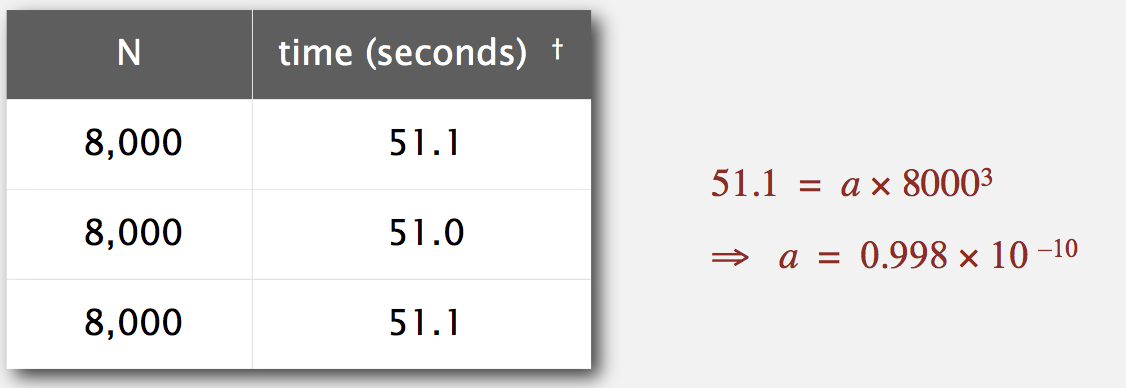
常用公式

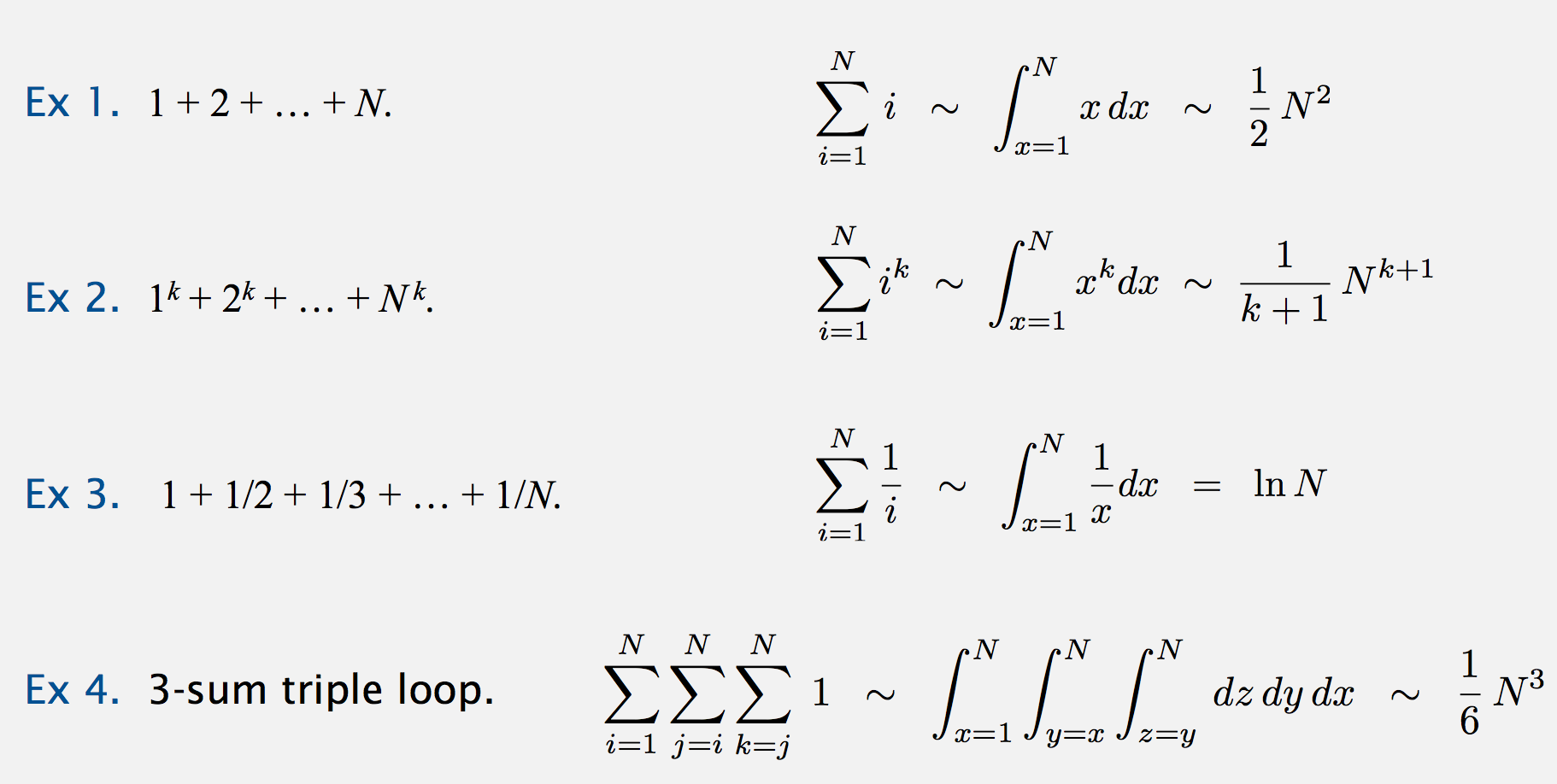
log-log plot 对应 复杂度

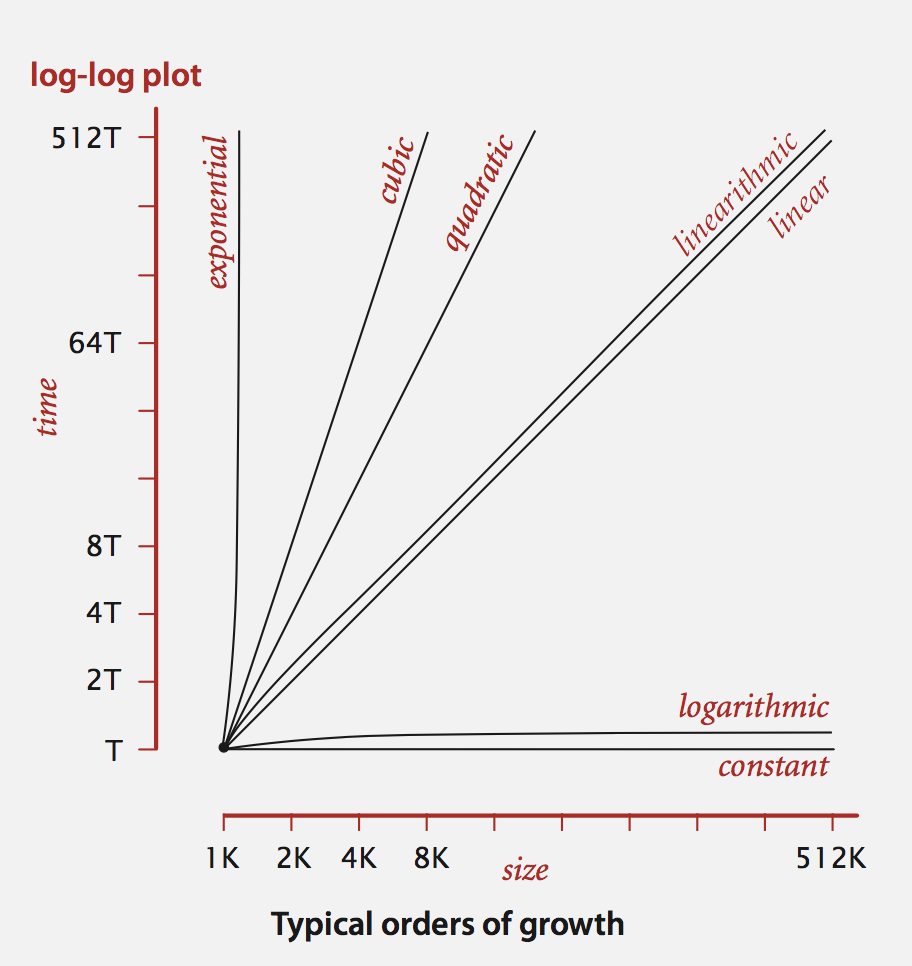
常见复杂度

复杂度对比

Cases

• Best case. Lower bound on cost.
• Worst case. Upper bound on cost.
• Average case. “Expected” cost.

衡量算法的方式

• 看最差：design for the worst case.
• 算预期：randomize, depend on probabilistic guarantee.

常用衡量符号

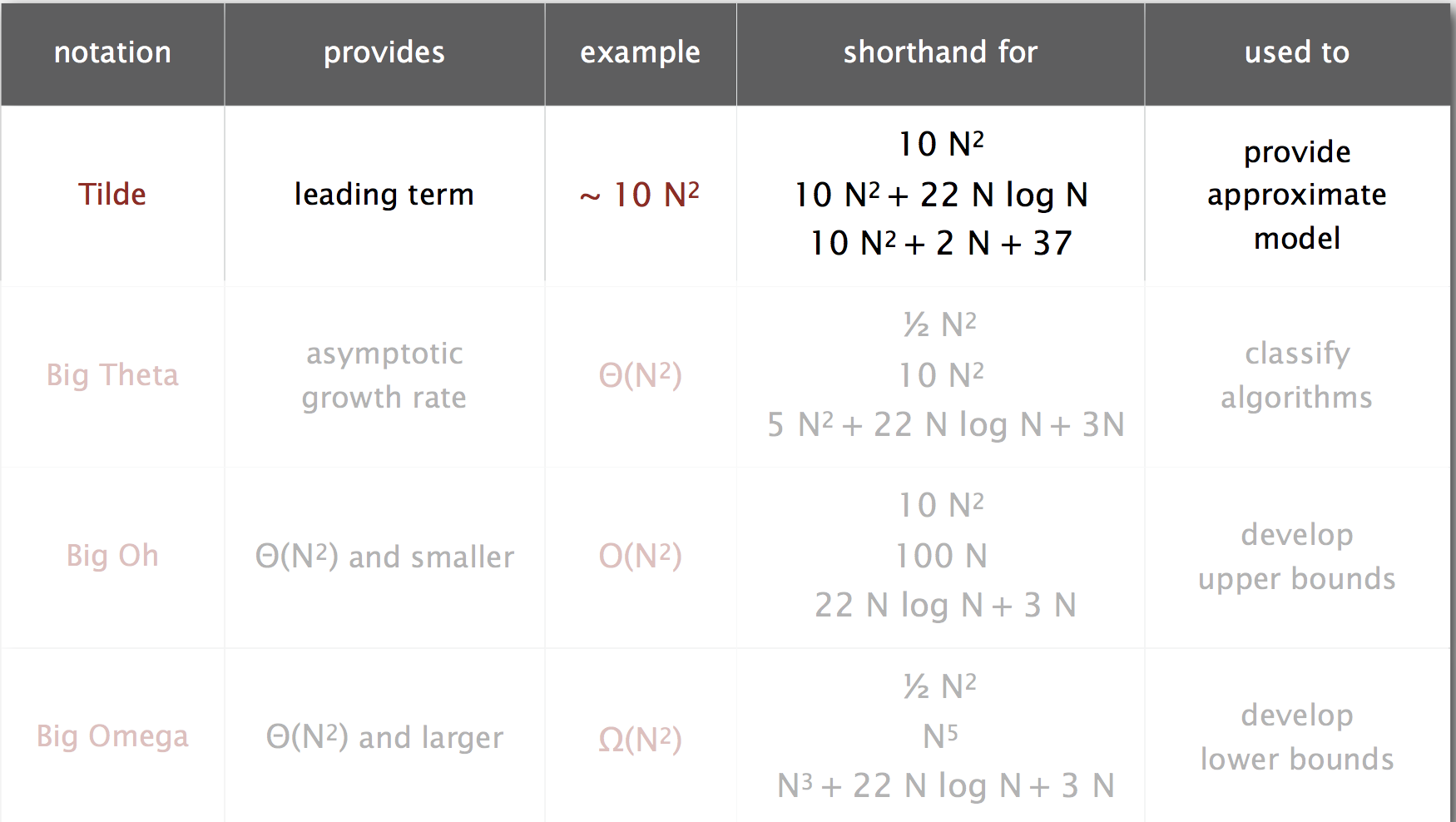
衡量一个具体问题的复杂度的例子

Goals

• Establish “difficulty” of a problem 确定一个问题的复杂度（不是算法的复杂度）
• Develop “optimal” algorithms.
• Ex. Q: 1-SUM(“Is there a 0 in the array? ”)

Upper bound. of A specific algorithm.

• Ex. Brute-force algorithm for 1-SUM: Look at every array entry.
• Running time of the optimal algorithm for 1-SUM is O(N).

对于一个确定算法——“依次寻找每个值”，它的最坏情况下（如果每个都不是0）的复杂度，是 O(N)

Lower bound. Proof that no algorithm can do better.

• Ex. Have to examine all N entries (any unexamined one might be 0).
• Running time of the optimal algorithm for 1-SUM is Ω(N).

事实上，对于任何一个算法，都必须检查每个值，因此这个问题下的所有算法，它们的最好时间复杂度也是 O(N)，因此本问题的最低时间复杂度Ω，是 Ω(N)

Optimal algorithm.

• Lower bound equals upper bound
• Ex. Brute-force algorithm for 1-SUM is optimal: its running time is Big Theta of N.

于是我们获得结论，刚刚那个确定算法，的确是最佳算法了。

算法进化论

• 如果当前的 Upper bound 和 问题的实际最低复杂度 Lower bound 不相等，即中间还有 Gap， 那么就是说这个算法还有优化空间
• 新算法就要落在 Upper bound 和 Lower bound 之间，不能超过暨有的最优值。也就是说新算法肯定要比老算法强，以老算法为上限。

注意每个符号的意义，不要误将O(n)认为是算法复杂度，其实~(n)才是

Memory

Basic

• Bit. 0 or 1.
• Byte. 8 bits.
• 32-bit machine: with 4 byte (32/8=4) pointers
• 64-bit machine: with 8 byte pointers
• 32/64 diff: Can address more memory; Pointers use more space.