Question: Dynamic Connectivity

Q: Given two points, are there any path connecting them? We also connect points dynamically.

Modeling

• Reflexive: p is connected to p
• Symmetric: if p is connected to q, then q is connected to p
• Transitive: if p is connected to q and q is connected to r, then p is connected to r.
• Connected components: Given points, we can create connected componenets. Then we should deal with the question: Is P and Q connected?

e.x: {0} {1,2,3} {4,5}: in each set points and muturally connected. If we connect 2 and 5, we can achieve a c.c: {0} {1,2,3,4,5}

Anwser 1: Quick find

• For {0} {1,2,3}, we give them different Component ID: 0, 1. So 0 has a CID of 0. 1,2, and 3 have a CID of 1.

• When we need to figure out whether two points and connected. We can check if they have the same CID.

• Futher more, we can decided the CID just by the one of point number in the component since neither two of their numbers equals.

• Data structure:

  Array: [id] = groupID

  The ID represents each number of the point and value represents CID.

  e.x. For {0} {1,2,3} {4,5} we have:

         0  1  2  3  4  5
  id[]   0  2  2  2  5  5
  

  There are 3 different components.

Code

public class QuickFindUF
{
    private int[] id;
    // init
    public QuickFindUF(int N)
    {
        id = new int[N];
        for (int i = 0; i < N; i++)
        {
            id[i] = i;
        }
    }
    public boolean connected(int p, int q)
    {  return id[p] == id[q];  }
    public void union(int p, int q)
    {
        int pid = id[p];
        int qid = id[q];
        for (int i = 0; i < id.length; i++)
            if (id[i] == pid) id[i] = qid;
    }
}

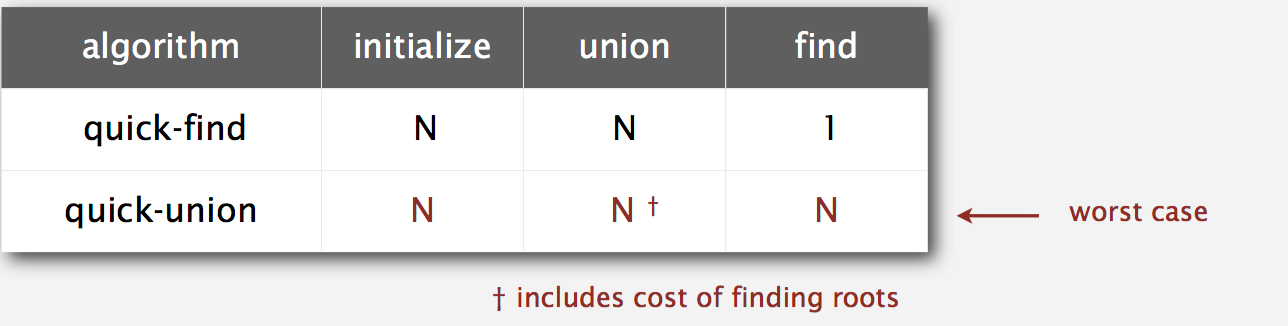
Cost

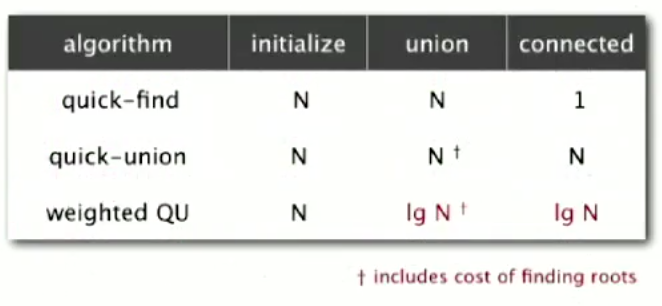
Union

N: Each call of union() need at most N times of comparing and changing.

For N points, its cost’s N^2.

Find

1: Checking two value only.

Initiallize

N: Each one has to been given a value.

Summary

We can’t accept quadratic time algorithms for large problems. The reason is they don’t scale. As computers get faster and bigger, quadratic algorithms actually get slower.

This algorithm can find quickly, so we call it Quick Find. But its unioning speed is too slow.

Answer 2: Quick union

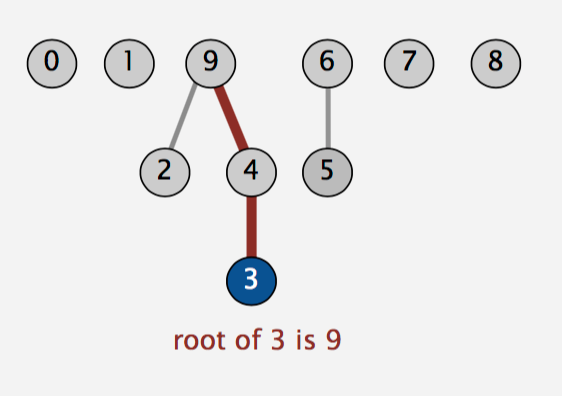
Treat these point as trees(forest):

e.x. {0} {1} {2,3,4,9} {5,6} {7} {8} ->

Data Structure

Array: [id] = itsParent

Algorithm

Operation union() is faster by:

For each union(), treat the first element as child, and the other as parent.

e.x. union(9,6):

In this case, we only need to change one value whatever the situation.

Code

public class QuickUnionUF
{
    private int[] id;
    // init
    public QuickUnionUF(int N)
    {
        id = new int[N];
        for (int i = 0; i < N; i++) id[i] = i;
    }
    private int root(int i)
    {
        while (i != id[i]) i = id[i];
        return i; 
    }
    public boolean connected(int p, int q)
    {
        return root(p) == root(q);
    }
    public void union(int p, int q)
    {
        int i = root(p);
        int j = root(q);
        id[i] = j;
    } 
}

Cost

Connected

N: for each point, one call for root costs at most N times(include cost of root equals root comparison). So it’s 2N. ->N.

Union

N: each union() operation call for root costs at most N times(include cost of root equals root comparison). So it’s 2N. ->N.

Summary

Quick-find defect

• Union too expensive (N array-accesses).
• Trees are flat, but too expensive to keep them flat.

Quick-union defect

• Trees can get tall.
• Find too expensive (could be N array accesses).

Answer 3: Weighted Quick-union

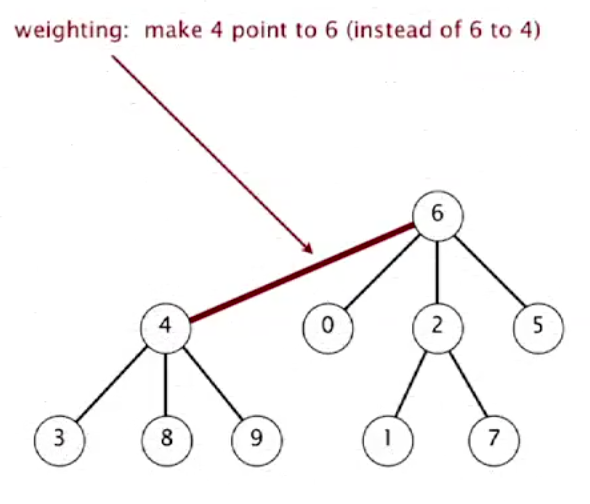
Modify quick-union to avoid tall trees. Balance by linking root of smaller tree to root of larger tree. So we can get a lower depth of tree.

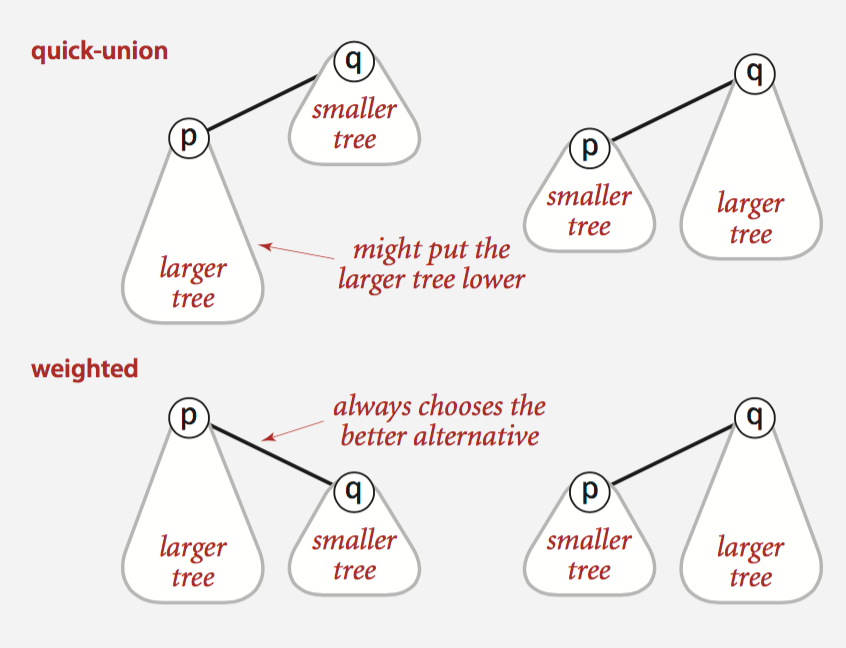
How to ensure each node has a lower depth?

While unioning two trees, we just let the smaller(by numbers of size) one to below the bigger one.

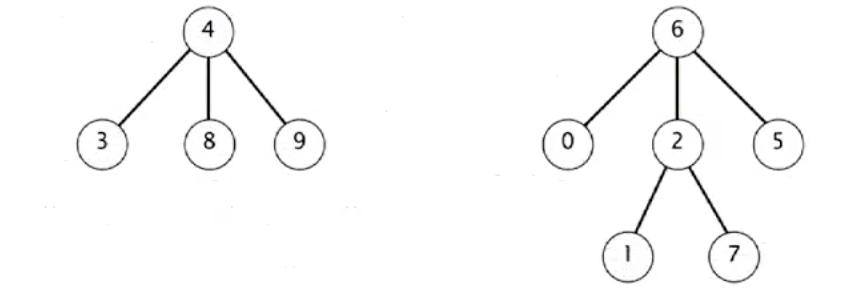
e.x.

after union(7,3)

Why this works?

• For each union() , the smaller tree get 1 depth increase, and larger one get nothing change. So the deepest tree of all maybe increase by 1.(assume that there are two deepest trees share the same depth)

• For each union() , the nodes of the smaller tree will at lease double, since the larger tree has no nodes less than that.

• Let’s assume that these nodes will be unioned into one singal tree to make the tree as deep and large as possible.

• Pick one random tree for example, T. For each union() , it may increase 1 depth or not. If it increase every time(the extreme situation), its nodes will double(at least) every time. T can double at most lg(log2) N times. Because:

  2^(lg N) = N

  After double lg N times, its number of node will increase to N, the total number of nodes.

• As a result, even if T adds depth every time union() , depth of T is at most lg N.

  lg x = log(2,x)

Cost

Initialize

N: id[] + sz[] = 2N -> N.

Union(each)

lg N: T(root()) = lg N

Connectted

lg N: T(root()) = lg N

Other improvements

Path compression

For every node call root(), it will make this node connect directly to root.

Summary

Ref

• Algorithms, Part I @Princeton, Coursera

• Algorithms, 4th Edition